Normally, a basic pagination often only includes Previous and Next buttons. But what if you have to navigate through thousands of pages every day?
If you browse popular e-commerce sites like Amazon or PlayStation Store, you’ll notice that they provide numbered pages in between.

This small detail makes browsing through a large catalog much more convenient.
Structure
Pagination consists of Page Operators and Pages.
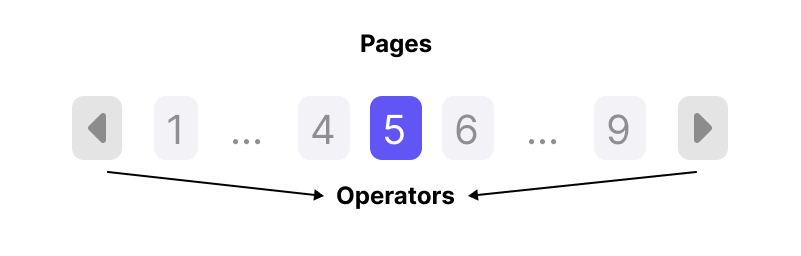
Here, we assume a total of 9 pages. Let’s walk through the pagination process from the first page to the last page.

Pagination Window and Pointer Model
We can observe the following:
Unchanged elements: the first page, the last page, and the current page window [n-1, n, n+1].
Therefore, we treat the first and last pages separately and only consider the middle pages.
Changed behavior: as you may notice, there are two hidden pointers that define the pagination window. Under normal conditions, both pointers dynamically shift to n-1 and n+1.
With two boundary exceptions: when the pagination reaches the start, the left pointer remains at 2; Similarly, when it reaches the end, the right pointer stays at 8.

Window Transition Rules
Based on the structure and pointer behavior described above, we can observe that the key consideration lies in how the start and end boundaries of the window are defined.
For example, if we want the ellipsis to be visible when the page distance is greater than 2, then when the distance between page n−1 and the first page is less than 2, the middle pages are displayed directly; otherwise, they are replaced by an ellipsis (...).
Based on this observation, the pagination logic can be formalized into a set of deterministic window transition rules.
| Mode | Condition | Pointer Status | Range | Description |
|---|---|---|---|---|
| A. Normal | start = n-1, end = n+1 | […, n-1, n, n+1, …] | The window follows the current page n, with ellipses on both sides. | |
| B. Reaches the start | n-1 ≤ 2 | start = 2, end = n+1 | n = 3, Range = [2, 3, 4, …] | The left pointer is fixed; the window expands to the right up to n+1. |
| C. Reaches the end | total - 1 - n + 1 ≤ 2 => total - n ≤ 2 | start = n-1, end = last-1 | n = 5, Range = […, 4, 5, 6, 7] | The right pointer is fixed; the window expands to the left down to n−1. |
Edge Cases
There is a special case where all page numbers should be displayed without any ellipsis. This occurs when the total number of pages is less than 6.
The threshold of 6 can be derived as follows:
(1 (first page) + 2 (window distance)) × 2,
since the pagination window is symmetric on both sides.
In addition, when the current page reaches either end (i.e., the first page or the last page), the window should expand beyond the normal range.
At the start, the window end is determined by:
max(1 + 2, n + 1)
At the end, the window start is determined by:
min(last − 2, n − 1)
These edge rules override the normal window transition logic to ensure a consistent and user-friendly pagination display.
Implementation
Algorithm Definition
The algorithm first handles edge cases, and then applies the window transition rules described above.
Input:
- currentPage (n)
- totalPages (total)
Output:
- start
- end
Algorithm:
-
If
total ≤ 6:start = 2end = last − 1
-
Else if Reaches the start:
start = 2end = max(3, n + 1)
-
Else if Reaches the end:
end = last − 1start = min(last − 2, n − 1)
-
Else:
start = n − 1end = n + 1
From these conditions, two boolean flags can be derived:
isCloseToStart = (n − 1 ≤ 2)isCloseToEnd = (total − n ≤ 2)
Code Implementation
Based on the window and pointer model described above, the JavaScript implementation can be viewed as a direct translation of the window transition rules into deterministic boundary calculations.
Core Function
We define a pure function that accepts the current page and total pages, and returns the calculated window range.
function getPaginationWindow(currentPage, totalPages) { const last = totalPages
// Edge case: small total size, no ellipsis required if (totalPages <= 6) { return { start: 2, end: last - 1 } }
const isCloseToStart = currentPage - 1 <= 2 const isCloseToEnd = totalPages - currentPage <= 2
// Reaches the start boundary if (isCloseToStart) { return { start: 2, end: Math.max(3, currentPage + 1) } }
// Reaches the end boundary if (isCloseToEnd) { return { start: Math.min(last - 2, currentPage - 1), end: last - 1 } }
// Normal sliding window return { start: currentPage - 1, end: currentPage + 1 }}Interactive Demo
Conclusion
This experience meant a great deal to me. After solving countless algorithm problems, I finally had the opportunity to apply those ideas to a real-world project.
This pagination problem, in particular, was something I had discussed with Gemini many times, yet I kept running into subtle bugs. Being able to resolve it cleanly on my own felt especially rewarding (I can even say I “defeated” Gemini this time…lol)
I hope this article proves helpful to others who encounter similar challenges.